범주형 Y에서 선형함수의 한계
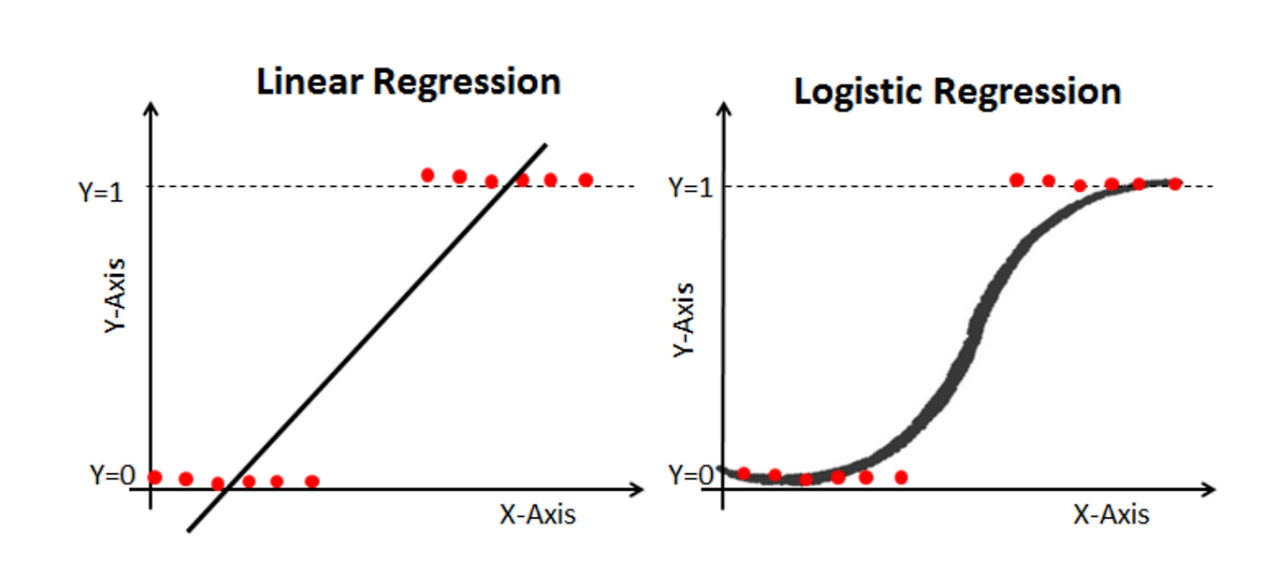
- X가 연속형 변수이고 Y가 특정 값이 될 확률이라고 설정한다면 선형으로 설명하기 쉽지 않음
- 확률은 0과 1 사이인데 예측값이 확률 범위를 넘어갈 수 있는 문제가 있음
- S자 형태의 함수를 적용하면 설명 가능
로짓 개념의 등장
- 오즈비(Odds ratio) 개념 적용
: 실패확률 대비 성공확률
- Logit
: P는 확률 값으로 0과 1 사이의 값인데 P가 증가할수록 오즈비가 급격하게 증가하기 때문에 선형성을 따르지 않음
따라서 log를 씌워 이 부분을 완화
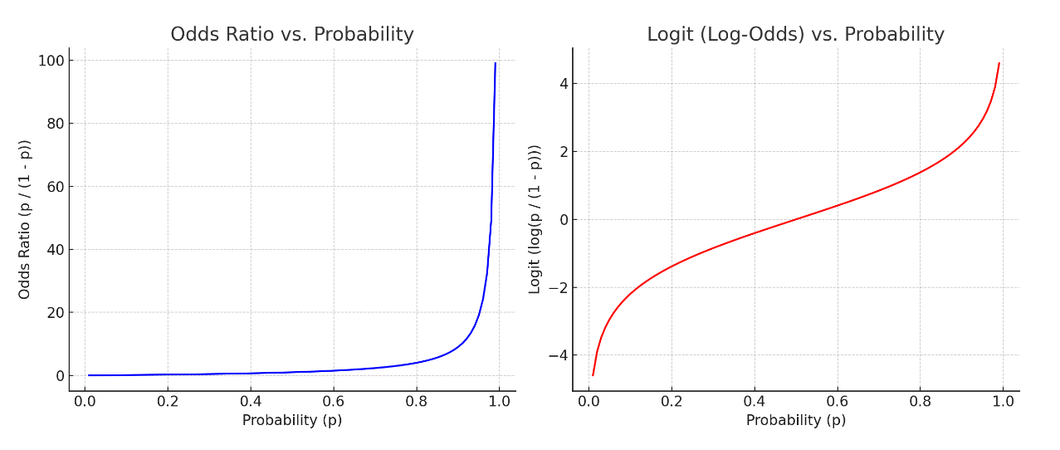
- 오즈비와 확률의 관계 / 로짓과 확률의 관계
- 로짓 그래프가 더 선형적인 그림을 나타내어 선형회귀의 기본식을 활용할 수 있게 됨
- 확률이 증가할수록 오즈비(좌)는 급격히 발산, 로짓(우)은 완만하게 증가
- 위의 확률-로짓 그래프 X-Y축 교체 / 로지스틱 함수

- 로짓과 기존 선형회귀의 우변을 합쳐 다음과 같은 식 도출

- 로짓의 장점은 어떤 값을 가져오더라도 반드시 특정 사건이 일어날 확률(Y값이 특정 값일 확률)이 0과 1 사이로 들어오게 하는 특징을 가지게 된다.
- 로지스틱함수는 가중치 값을 안다면 X값이 주어졌을 때 해당 사건이 일어날 수 있는 P의 확률을 계산할 수 있게 됨
정확도의 한계
- 극단적인 예시
: 암 예측 모델 - 모든 환자가 음성(정상인)이라고 판정- 100명의 환자 입실, 95명은 음성(정상), 5명은 양성(암 환자)
- 위의 경우 암 예측 모델의 정확도는 95%
- 그러나 실제 양성(암 환자)는 하나도 맞추지 못함
혼동 행렬(Confusion Matrix)
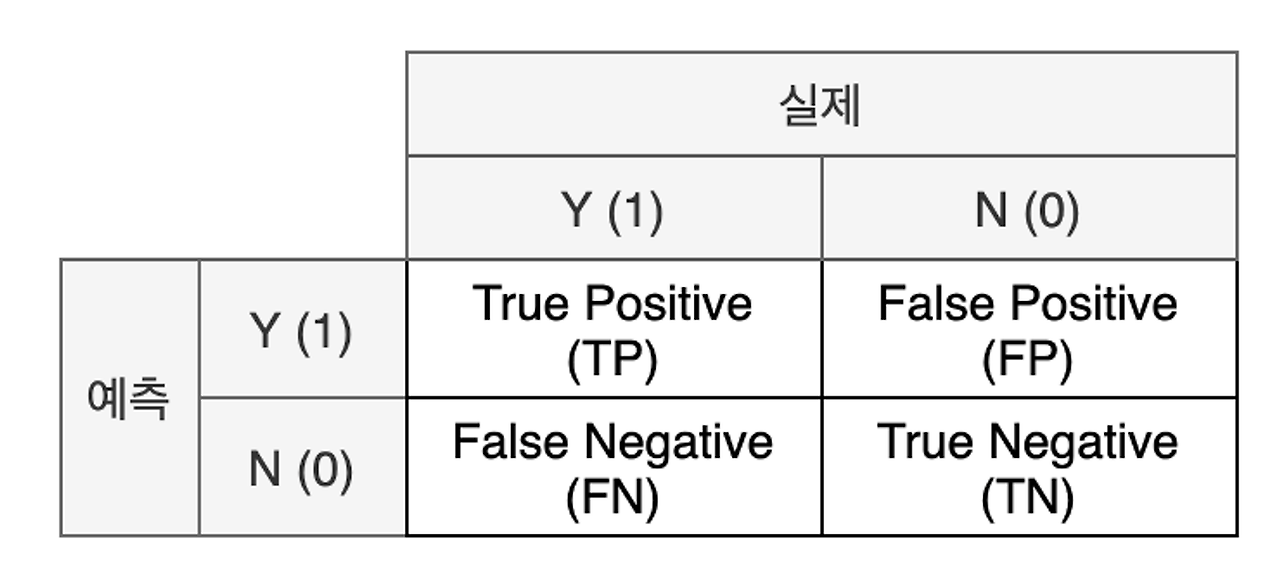
- 실제 값과 예측 값에 대한 모든 경우의 수를 표현하기 위한 2x2 행렬
- 표기법
- 실제와 예측이 같으면 True, 다르면 False
- 예측을 양성으로 했으면 Positive, 음성으로 했으면 Negative
- 해석
- TP: 실제로 양성(암 환자)이면서 양성(암 환자) 올바르게 분류된 수
- FP: 실제로 음성(정상인)이지만 양성(암 환자)로 잘못 분류된 수
- FN: 실제로 양성(암 환자)이지만 음성(정상인)로 잘못 분류된 수
- TN: 실제로 음성(정상인)이면서 음성(정상인)로 올바르게 분류된 수
- 지표
- 정밀도(Precision) : 모델이 양성 1로 예측한 결과 중 실제 양성의 비율(모델의 관점)

- 재현율(Recall) : 실제 값이 양성인 데이터 중 모델이 양성으로 예측한 비율(데이터의 관점)
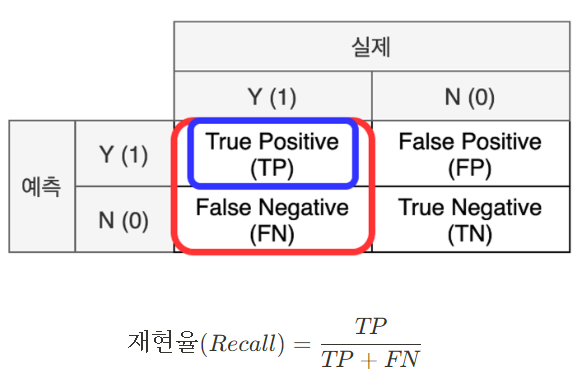
- F1-Score : 정밀도와 재현율의 조화 평균

- 정확도(Accuracy)

- 정밀도(Precision) : 모델이 양성 1로 예측한 결과 중 실제 양성의 비율(모델의 관점)
- 암 예측 모델에 적용
- TP: 실제로 양성(암 환자)이면서 양성(암 환자) 올바르게 분류된 수 → 0명
- FP: 실제로 음성(정상인)이지만 양성(암 환자)로 잘못 분류된 수 → 0명
- FN: 실제로 양성(암 환자)이지만 음성(정상인)이라고 분류된 수 → 5명
- TN: 실제로 음성(정상인)이면서 음성(정상인)이라고 분류된 수 → 95명
- 정밀도는 정의되지 않음(divsion by zero), 재현율은 0
- 결과적으로 f1-score는 0
- 위처럼 정확도가 제 기능을 못하는 때(특히 Y값이 unbalance 할 때)에는 Y 범주의 비율을 맞춰주거나 평가 지표를 F1-Score를 사용함으로써 이를 보완
'스파르타 코딩클럽 > [강의] 머신러닝' 카테고리의 다른 글
| [머신러닝 심화] 데이터 분석 프로세스 - 데이터 수집 및 EDA (0) | 2024.01.31 |
|---|---|
| [머신러닝 기초] 회귀와 분류 정리 (0) | 2024.01.30 |
| [머신러닝 기초] 선형회귀의 가정과 정리 (2) | 2024.01.30 |
| [머신러닝 기초] 다중선형회귀와 범주형 데이터 실습 (0) | 2024.01.30 |
| [머신러닝 기초] 선형회귀 실습 (0) | 2024.01.30 |